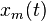 và sóng mang cao tần hình sin
và sóng mang cao tần hình sin 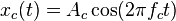 ,
ở đây fc là tần số sóng mang cao tần và Ac là biên độ sóng mang cao
tần. Bộ điều chế kết hợp sóng mang với tín hiệu băng gốc để có được tín
hiệu truyền là:
,
ở đây fc là tần số sóng mang cao tần và Ac là biên độ sóng mang cao
tần. Bộ điều chế kết hợp sóng mang với tín hiệu băng gốc để có được tín
hiệu truyền là: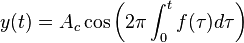
![= A_{c} cos left(2 pi int_{0}^{t} left[ f_{c} + f_{Delta} x_{m}( au)
ight] d au
ight)](https://upload.wikimedia.org/math/d/7/4/d744f3f0b1df05a7bfa450c7eadec1f2.png)
 Trong phương trình này,
Trong phương trình này,  là tần số tức thời của bộ tạo dao động và
là tần số tức thời của bộ tạo dao động và  là độ lệch tần số đặc trưng của may bien tan cho độ lệch cực đại so với fc trên một hướng, giả sử xm(t) có giới hạn trong khoảng (-1, +1).
là độ lệch tần số đặc trưng của may bien tan cho độ lệch cực đại so với fc trên một hướng, giả sử xm(t) có giới hạn trong khoảng (-1, +1).Mặc dù có vẻ như điều này giới hạn tần số sử dụng trong khoảng fc ± fΔ, nó bỏ qua sự khác biệt giữa tần số tức thời và phổ tần số. Phổ tần số của một tín hiệu FM thực tế có phần mở rộng ra đến vô cùng, chúng trở nên rất nhỏ khi vượt qua một điểm.
Một tín hiệu điều chế băng gốc có thể xấp xỉ bằng một tín hiệu hình sin liên tục với tần số fm. Tích phân của tín hiệu này là
 Vì vậy, trong trừong hợp cụ thể này, phương trình (1) ở trên có thể đơn giản hóa thành:
Vì vậy, trong trừong hợp cụ thể này, phương trình (1) ở trên có thể đơn giản hóa thành: ở đây biên độ
ở đây biên độ  của tín hiệu hình sin điều chế được biểu diễn bằng độ lệch đỉnh
của tín hiệu hình sin điều chế được biểu diễn bằng độ lệch đỉnh  (xem độ lệch tần số).
(xem độ lệch tần số).Sự phân bố hài hòa của sóng mang hình sin được điều chế bởi một tín hiệu dạng sin có thể được biểu diễn bằng các hàm Bessel - hàm này cung cấp một cơ sở hiểu biết toán học của điều chế tần số trong miền tần số.
